En Busca del Modelo Perdido - Parte 6: La Primera Reliquia

La odisea continúa en “En Busca del Modelo Perdido”, y en este episodio, titulado “La Primera Reliquia”, desvelamos un hallazgo crucial en nuestro viaje hacia un modelo robusto de predicción de resultados de la PAES a nivel escolar.

🧭 Descifrando el Mapa hacia la Primera Reliquia 🗺️

Nuestro viaje en el universo del análisis de datos nos lleva a un descubrimiento esencial: la afinación precisa de nuestro modelo Random Forest. Al profundizar en los secretos de la programación y sus impactos, hemos dado con un dato clave: el heatmap que relaciona la precisión del modelo con los valores de n_estimators y num_folds. El análisis de este gráfico es crucial para definir el modelo que nos dará la confiabilidad necesaria para establecer las predicciones finales.

🌟 El Desafío de los Parámetros: n_estimators y num_folds

El corazón de nuestra indagación se centra en dos parámetros cruciales: n_estimators y num_folds en la validación cruzada. La elección no es trivial, ya que cada ajuste puede influir significativamente en la precisión y eficiencia de nuestro modelo.

🌐 Patrones en el Heatmap: Folds como Factor Dominante

Al analizar el heatmap interactivo de MAE, un patrón interesante salió a la luz: la dependencia de los resultados con el número de folds. Observamos patrones horizontales claros, lo que indica que el número de folds tiene un impacto más significativo en el MAE que el número de estimadores.

Este hallazgo fue crucial para nuestro análisis. Aunque los n_estimators tienen cierta influencia, especialmente hasta el valor de 200, cualquier número más allá de este punto no parecía afectar significativamente los resultados del modelo (no hay líneas verticales que hablen de fluctuaciones significativas). Esto sugiere que alcanzamos un límite en la precisión del modelo con respecto a n_estimators, y la atención debería centrarse en optimizar el número de folds para un equilibrio adecuado entre precisión y generalización.

Imagen 1 (visible en computadores): Heatmap interactivo que muestra cómo varían los valores de MAE con diferentes combinaciones de 'n_estimators' y 'num_folds'.

📐 Ajustando el Enfoque: MAE, Folds y Estimadores 📊

Continuando en nuestro periplo, el análisis de la estabilidad de los valores de folds se hizo imprescindible. Como puedes notar en el gráfico interactivo, los valores de 3, 5 y 14 en la cantidad de folds parecen mostrar los valores más bajos y significativos para MAE. Utilizamos un gráfico de dispersión para entender mejor cómo el MAE cambia con diferentes números de estimadores y estos valores para los folds. El resultado se muestra a continuación.

Imagen 2: Análisis de la Estabilidad de los Folds 3, 5 y 14 en función del número de estimadores.

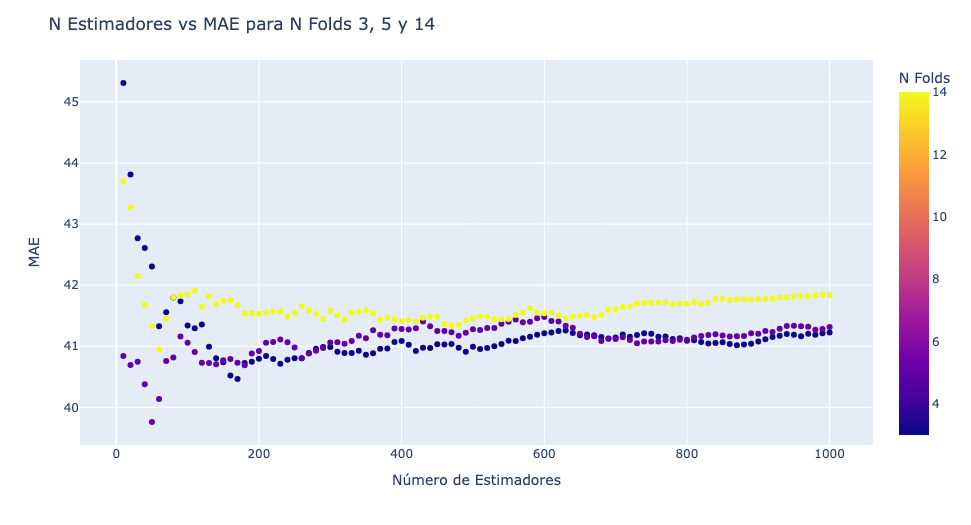
Este gráfico me ayudó a comprender la relación entre el número de estimadores y el MAE para cada uno de estos números de folds específicos. A manera de análisis, creo que es importante que notes que los folds 3 y 5 tienden a minimizar el MAE a partir del valor 700 aproximadamente. El fold 14 (color amarillo) se mantiene ligeramente más arriba que estos dos lo cual hace que descartemos su uso.

En vista de que hay una estabilidad importante para los fold 3 y 5 en el rango de 600 y 1000 de n_estimators seleccioné un valor intermedio para asegurar de alguna manera la estabilidad del modelo (no cerca del borde inferior o exterior del rango). Como una mayor cantidad de folds ayuda a mejorar la generacionación y entrenamiento del modelo, entonces privilegiamos 5 por sobre 3.

🧐 Justificación de la Elección: Equilibrio entre Precisión y Generalización

Por el análisis anterior, nuestra elección se basa en una justificación sólida. La combinación de n_estimators=800 y num_folds=5 no solo mostró un MAE mejor que el promedio, sino que también indicó estabilidad y robustez. Esta configuración asegura que el modelo es preciso, pero también generalizable a nuevos datos, un equilibrio crucial en la ciencia de datos.

🛠️ Construyendo el Modelo: El Código Final 🧑‍💻

Después de un análisis detallado y la elección cuidadosa de los parámetros, procedimos a construir el modelo final de Random Forest. El siguiente código refleja la culminación de nuestros esfuerzos:

import numpy as np
import pandas as pd
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import cross_val_predict, KFold
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt

# Cargar los datos desde el archivo CSV
csv_filename = "PAES_training_set_2022_Complete - PAES_training_set_2022 - Matemáticas.csv"
data = pd.read_csv(csv_filename)

# Eliminar filas con valores faltantes
data = data.dropna()

# Convertir columnas numéricas a tipos de datos numéricos
numeric_columns = data.columns.difference(['ID', 'Curso', 'Nombre', 'PAES'])
data[numeric_columns] = data[numeric_columns].astype(float)

# Dividir los datos en características (X) y objetivo (y)
X = data.drop(['ID', 'Curso', 'Nombre', 'PAES'], axis=1)
y = data['PAES']

# Normalizar los datos
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# Construir el modelo Random Forest Regressor
rf_regressor = RandomForestRegressor(n_estimators=800, random_state=42)

# Crear objeto KFold con el número de folds deseado
num_folds = 5
kf = KFold(n_splits=num_folds)

# Realizar validación cruzada con cross_val_predict
y_pred = cross_val_predict(rf_regressor, X_scaled, y, cv=kf)

# Obtener la importancia de las características
rf_regressor.fit(X_scaled, y)
feature_importances = rf_regressor.feature_importances_

# Obtener las columnas correspondientes a las características
feature_columns = X.columns

# Obtener las 5 características más importantes
top_features_indices = feature_importances.argsort()[-5:][::-1]
top_features = feature_columns[top_features_indices]
top_feature_importances = feature_importances[top_features_indices]

print("Características más importantes:")
for i, (feature, importance) in enumerate(zip(top_features, top_feature_importances)):
    print(f"{i+1}. {feature}: {importance:.4f}")

# Gráfico de valores reales vs. predicciones
plt.figure(figsize=(10, 6))
plt.scatter(y, y_pred, alpha=0.5)
plt.xlabel('Valor Real de PAES')
plt.ylabel('Predicción de PAES')
plt.title('Valores Reales vs. Predicciones')
plt.grid()
plt.show()

Podrás notar que como valor agregado hemos hecho que se entreguen los elementos de la tabla original de datos que puedan ser más significativos para la construcción del modelo. Esto nos da luces de qué es lo que quizás pueda ocurrir a lo largo de ls ensayos o mediciones que podría ayudar a corregir el proceso de aprendizaje. El resultado de todo se muestra a continuación:

Resultados

Características más importantes:

1. EnsayoSeptiembre: 29.47%
2. EnsayoJunio: 23.83%
3. EnsayoOctubre: 14.60%
4. EnsayoNoviembre: 10.94%
5. EnsayoAgosto: 8.70%

Imagen 3: Resultado del modelo de random forest ajustado y valores reales obtenidos en la PAES. Los resultados muestran un ajuste con una desviación del orden de 50 puntos.

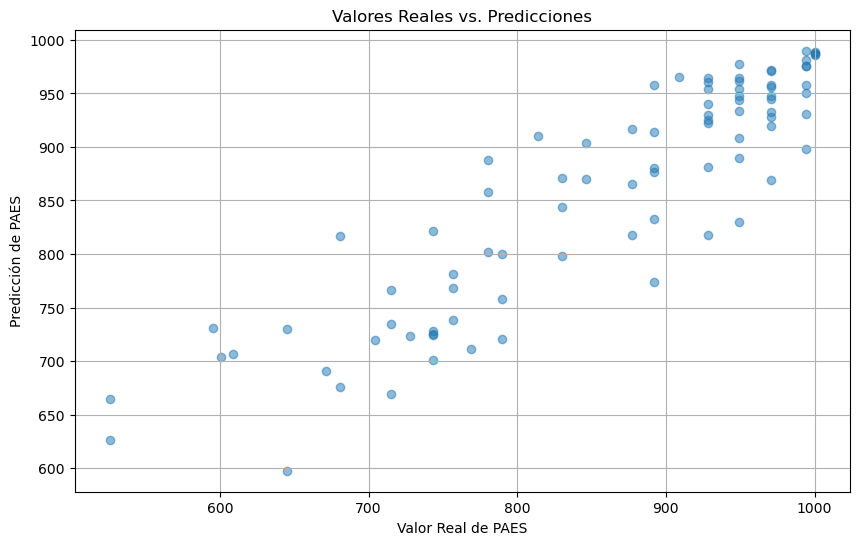
Este código incorpora la normalización de los datos, el uso de Random Forest con los parámetros seleccionados y la validación cruzada. Además, proporciona una visualización de las predicciones del modelo frente a los valores reales de PAES que concluyen con un excelente error de unos 50 puntos.

Puede parecer mucho, pero en los niveles en los que se tienen los resultados cada pregunta de la PAES pesa entre unos 17 y 20 puntos, por lo que el error de nuestro modelo de predicción es en el peor de los casos de 3 preguntas, lo cual es increíblemente notable considerando la base de datos que tenemos para partir.

Junto a lo anterior, se encuentran el aporte que hacen los factores más relevantes en la descripción del modelo. Como puedes notar, los elementos más importantes fueron algunos de los ensayos (y no la asistencia u otros elementos de la base de datos), lo cual parece consistente con nuestra intuición y posiblemente experiencia. Ahora bien, una persona a cargo del diseño de estos ensayos podría estar al tanto de los tiempos en que se juegan los resultados cruciales y motivar algún cambio que pueda impactar en los resultados finales.

Esto es solo un ejemplo de lo que se puede lograr con este simple ensayo. Si la base de datos aumenta con nuevas variables, el estudio de elementos clave en el proceso se hará visible y las decisiones apalancadoras del aprendizaje aflorarán.

📈 Análisis de Residuos: Comprendiendo el Error del Modelo

Para evaluar aún más el rendimiento de nuestro modelo, realizamos un análisis de residuos. Esto ayudará a entender dónde se concentraban los datos y a visibilizar el nivel de error del modelo de manera más clara.

Imagen 4: Analisis de residuos entre el modelo predictivo, los valores reales y la distribución de los resultados en cada eje.

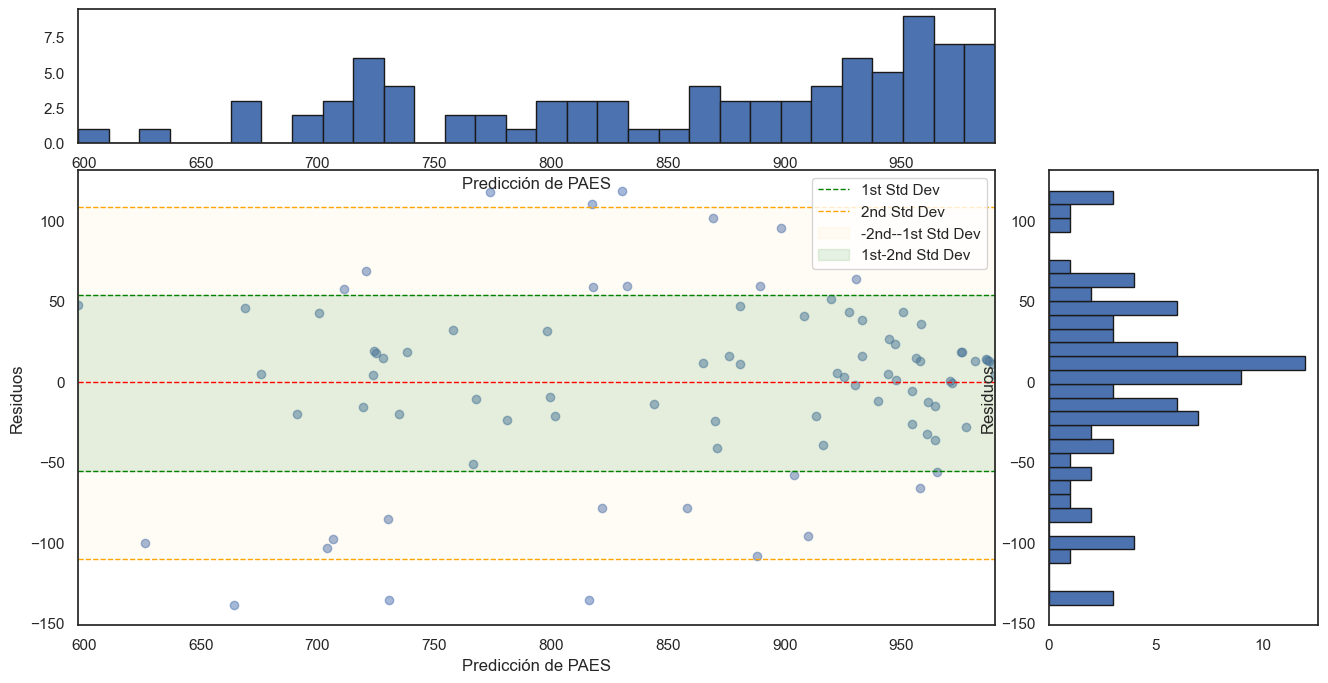
Este análisis gráfico nos proporciona una perspectiva detallada de la distribución de los errores de nuestro modelo. Aquí ya podemos notar que la confiabilidad del modelo es robusta ya que la mayoría de las diferencias se mueve en valores que van de -50 a 50 puntos.

La mayor población de resultados se mueve en un rango superior a los 850 puntos por lo que debemos considerar que esta es una población de estudiantes que en general tuvieron buenos resultados en la prueba PAES. Para mejorar los rangos inferiores habría que tener más datos y de estudiantes con esas realidades para así afinar más la predicción.

🚀 Hacia el Futuro: La Importancia de la Primera Reliquia

Este descubrimiento, la Primera Reliquia, no es solo un paso en nuestra saga, sino una base sólida para futuras exploraciones. Con un modelo bien afinado, estamos más cerca de desvelar los secretos de la PAES y su predicción a nivel escolar. Esto ayudará sin duda a que las autoridades que tienen a cargo instituciones educativas o procesos de gestión en el aprendizaje tengan claridad de qué parametros deben “mover” para maximizar el aprendizaje de sus estudiantes y así entregar más oportunidades a sus vidas.

Por fin, esto ya no se trata solo de un asunto de “percepciones” que la mayor parte del tiempo carecen de un fundamento claro en la toma de decisiones. Enfocar el aprendizaje con herramientas de este tipo favorece sin dudas la claridad en los procesos de aprendizaje que pueden estar afectando los desempeños. Si podemos aplicarlo esta primera vez par ala PAES, podemos por supuesto aplicarlo a todas las prácticas pedagógicas.

En el próximo capítulo, continuaremos nuestra aventura, llevando nuestra Primera Reliquia hacia nuevos horizontes y desafíos. Manténganse atent@s, aprendanzantes, la búsqueda continúa…

Hasta el próximo cronopunto del Principia 🥚.

DV