En Busca del Modelo Perdido - Parte 5: Afinando el Random Forest
Continuando nuestra exploración en el mundo del análisis de datos, nos enfrentamos ahora al desafío de afinar nuestro modelo de Random Forest. En este capítulo, nos centramos en entender mejor las decisiones detrás de nuestra programación y el impacto que tienen en los resultados finales.
🎓 Comprendiendo el Porqué Detrás del Código 🎓
Cada línea de código en un análisis de datos tiene un propósito y puede influir significativamente en el resultado final. Es esencial entender el ‘porqué’ detrás de cada función y parámetro para ser capaz de confiar y explicar los resultados de nuestro modelo.
Para no olvidar nuestro trabajo hasta ahora, te comparto el código que dejamos en el capítulo 3:
A pesar de ser un código que entrega resultados prometedores, aún nos falta saber si es posible acercarnos a un nivel de confiabilidad superior y conciente. Para lograr esto último, comenzaremos entonces por analizar las piezas de código que son fundamentales.
¿Por qué dividimos los datos?
from sklearn.model_selection import train_test_split
# Dividimos los datos en conjuntos de entrenamiento y prueba
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
La función ‘train_test_split’ es una herramienta que divide nuestros datos en dos partes: un conjunto para entrenar nuestro modelo y otro para probarlo. El test_size=0.2 significa que el 20% de los datos se reservan para probar el modelo, mientras que el resto se utiliza para el entrenamiento.
Pero, ¿por qué 20% y no otro número? Elegir el tamaño del conjunto de prueba es una decisión que puede afectar la precisión de nuestras predicciones. Un conjunto de prueba demasiado pequeño puede no capturar la variabilidad de los datos, mientras que uno demasiado grande podría no dejar suficientes datos para entrenar el modelo adecuadamente.
Esto último es la razón por la que este mecanismo de separación de los datos puede no ser el mejor para generalizar nuestro modelo.
La Importancia de ‘n_estimators’ y ‘random_state’
from sklearn.ensemble import RandomForestRegressor
# Creamos el modelo de Random Forest
model = RandomForestRegressor(n_estimators=100, random_state=42)
El parámetro n_estimators determina cuántos árboles incluir en nuestro bosque. Cien árboles es un buen punto de partida, pero no hay una respuesta única para todos los casos. Es evidente que mientras más árboles decidimos usar el modelo “podría mejorar” ya que la cantidad de posibles caminos considerados es mayor, pero también requeriremos más potencia de cómputo. Debemos equilibrar la complejidad del modelo con la capacidad de generalizar bien a nuevos datos para así no usar recursos innecesarios y hacer que el código sea también ágil.
El random_state es nuestra semilla de aleatoriedad. Utilizar un número fijo, como 42, garantiza que si repetimos el análisis obtendremos los mismos resultados cada vez que corremos el código. Esto es crucial para la reproducibilidad de nuestro estudio y no sacar conclusiones diferentes por cada vez que vemos los resultados del output.
🔍 Refinando la Validación del modelo: Superando la División Estática 🔍
La división estándar de los datos en un 80% para entrenamiento y un 20% para pruebas no siempre captura la complejidad y variabilidad inherentes en nuestro conjunto de datos. Para mejorar nuestra evaluación del modelo y asegurarnos de que es robusto y confiable, implementamos una técnica llamada “validación cruzada”.
from sklearn.model_selection import cross_val_score, KFold
# Configuramos la validación cruzada
kf = KFold(n_splits=5)
cross_val_scores = cross_val_score(model, X, y, cv=kf)
La función ‘KFold’ de ‘sklearn’ nos permite dividir el conjunto de datos en múltiples segmentos o ‘folds’. A diferencia de una única división de entrenamiento/prueba, la validación cruzada evalúa el modelo en varias rondas, utilizando cada vez un segmento diferente como conjunto de prueba y el resto como entrenamiento. Esto garantiza que cada muestra de los datos se utilice tanto para entrenar como para validar el modelo, dándonos una medida más fiable de su rendimiento y evitando que ciertas peculiaridades de los datos influyan de manera desproporcionada en los resultados. En palabras simples, le da a todos los datos disponibles la posibilidad de ser parte del grupo de entrenamiento y también del de prueba.
Esto consumirá una cantidad de recursos de procesamiento mucho mayor, pero también es una ganancia enorme en confiabilidad del modelo por lo que se sugiere muy fuertemente utilizar mecanismos de ésta índole.
Analizando el Error Absoluto Medio (MAE)
Una parte esencial en la afinación de nuestro modelo Random Forest es la elección de cuántos ‘folds’ o particiones usar en la validación cruzada. Esta decisión puede influir significativamente en la confiabilidad de las predicciones que hacemos. Para guiar esta elección, recurrimos al concepto de Error Absoluto Medio (MAE), que nos ofrece una medida directa de cuánto se desvían nuestras predicciones de los valores reales.
El MAE es la diferencia promedio entre el valor predicho y el valor real. En otras palabras, nos dice cuánto se equivoca nuestro modelo, en promedio, en las predicciones que hace. Un MAE bajo indica que nuestras predicciones son precisas, mientras que un MAE alto sugiere que podríamos estar bastante lejos del objetivo.
Explorando el número óptimo de ‘folds’
Para encontrar el número óptimo de ‘folds’, realizamos un experimento iterando a través de un rango de valores y calculando el MAE para cada uno. Aquí está el fragmento de código que lleva a cabo esta tarea:
from sklearn.model_selection import cross_val_score, KFold
from sklearn.ensemble import RandomForestRegressor
# Experimento con diferentes cantidades de 'folds'
for fold in range(2, 80):
# Configuramos el KFold con el número actual de 'folds'
kf = KFold(n_splits=fold)
# Inicializamos el modelo Random Forest con 100 estimadores
model = RandomForestRegressor(n_estimators=100)
# Calculamos el MAE para el número actual de 'folds'
# Usamos la validación cruzada para asegurarnos de que el cálculo del MAE es robusto
mae_score = -cross_val_score(model, X, y, cv=kf, scoring='neg_mean_absolute_error').mean()
# Imprimimos el número de 'folds' y el MAE correspondiente
print(f"{fold} folds: MAE = {mae_score}")
Cada iteración del bucle ‘for’ configura un nuevo objeto ‘KFold’ con un número diferente de ‘folds’ (que en este caso se mueve entre valores desde el 2 hasta el 80), que luego se utiliza para evaluar el modelo Random Forest. La función cross_val_score se emplea aquí para realizar la validación cruzada, y le pasamos el scoring parameter como ‘neg_mean_absolute_error’ porque queremos calcular el MAE negativo; luego lo negamos (multiplicamos por -1) para convertirlo en un valor positivo que podemos interpretar fácilmente.
Interpretando los Resultados con Visualizaciones
Tras realizar el experimento y calcular el MAE para cada número de ‘folds’, es hora de interpretar los resultados. Una forma efectiva de hacerlo es a través de la visualización de datos. Los gráficos nos permiten ver tendencias y patrones que pueden no ser evidentes solo con los números.
El siguiente código nos da una representación gráfica de cómo el MAE varía con el número de ‘folds’ utilizado en la validación cruzada:
import matplotlib.pyplot as plt
import seaborn as sns
# Gráfico de MAE promedio en función del número de folds
plt.figure(figsize=(10, 6))
sns.lineplot(x=num_folds_range, y=mae_scores_mean, marker='o')
plt.xlabel('Número de Folds de Validación Cruzada')
plt.ylabel('Error Absoluto Medio (MAE) Promedio')
plt.title('Análisis del Número de Folds en Validación Cruzada')
plt.grid()
plt.show()
El resultado de este experimento se muestra en el siguiente gráfico:
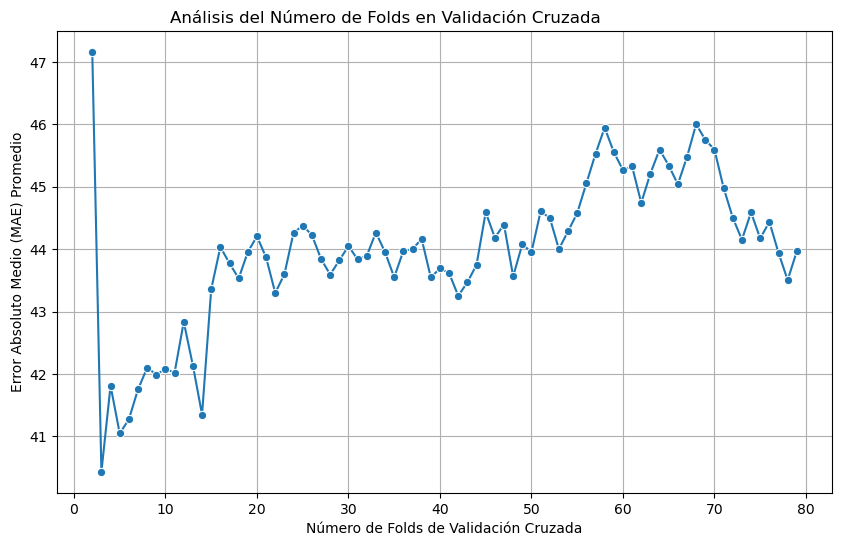
Como puedes ver, la precisión de nuestro modelo depende de los valores que tenga ‘KFold’ y es de gran importancia determinar cuál es el valor adecuado para nuestro modelo predictivo. Esto y saber cuáles fueron los criterios utilizados para definirlo.
En nuestro caso, utilizaré aquel KFold que minimice el valor de MAE, pero que tambien presente indicios de estabilidad en el modelo. Esto último se logra evidenciando sectores en que MAE sea constante dentro de este gráfico, o en palabras más simples, cuando el MAE no cambie demasiado si yo cambio KFolds.
📐 Ajustando el Enfoque: MAE, Folds y Estimadores 📊
A medida que avanzamos en el refinamiento de nuestro modelo, nos damos cuenta de que la evaluación del MAE no depende únicamente de la cantidad de ‘folds’. Hay otro factor en juego que puede ser igualmente importante: la cantidad de estimadores en nuestro Random Forest. De hecho me inquietó tanto el problema que hice un experimento similar al que hicimos con los ‘folds’ pero esta vez con el número de estimadores. El resultado fue el siguiente gráfico:
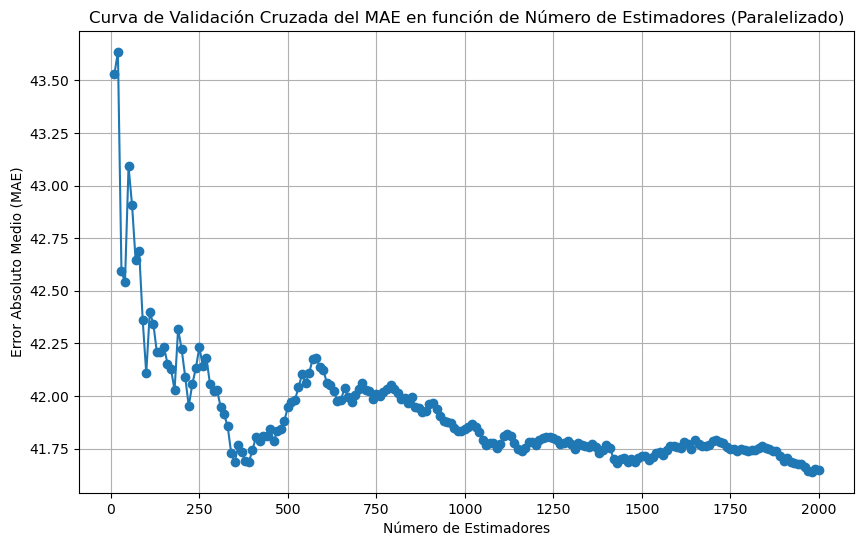
De lo que podemos ver, la precisión de las predicciones se ve claramente afectada por el número de árboles que estamos utilizando para construir el modelo.
Por lo tanto, nos enfrentamos a un análisis tridimensional donde debemos considerar ‘folds’, estimadores y MAE simultáneamente para optimizar nuestro modelo… y eso creo que puede ser el problema mas complejo de toda nuestra aventura 😨.
Explorando la Interacción entre Folds y Estimadores
Para abordar esta complejidad, ampliamos nuestro experimento para incluir un rango de estimadores. Aquí está el código que utilicé para paralelizar el cálculo del MAE promedio y considerando ambos factores:
from sklearn.model_selection import cross_val_score, KFold
from sklearn.ensemble import RandomForestRegressor
from joblib import Parallel, delayed
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# Rangos de número de estimadores y número de folds a explorar
n_estimators_range = list(range(10, 1001, 10))
num_folds_range = list(range(2, 81, 1))
# Función para calcular MAE promedio en paralelo para un número de folds y estimadores
def calculate_mae_mean(num_folds, n_estimators):
rf_regressor = RandomForestRegressor(n_estimators=n_estimators, random_state=42)
kf = KFold(n_splits=num_folds)
cv_mae_scores = -cross_val_score(rf_regressor, X, y, cv=kf, scoring='neg_mean_absolute_error')
mae_mean = cv_mae_scores.mean()
return mae_mean
# Paralelizar el cálculo del MAE promedio para diferentes números de folds y estimadores
num_cores = 4 # Define el número de núcleos a utilizar en paralelo
mae_scores_mean = Parallel(n_jobs=num_cores)(
delayed(calculate_mae_mean)(num_folds, n_estimators)
for num_folds in num_folds_range
for n_estimators in n_estimators_range
)
# Crear una matriz de valores de MAE en función de num_folds_range y n_estimators_range
mae_matrix = np.array(mae_scores_mean).reshape(len(num_folds_range), -1)
# Crear el mapa de calor
plt.figure(figsize=(12, 8))
sns.heatmap(mae_matrix, cmap="YlOrRd", annot=False, fmt=".2f", xticklabels=n_estimators_range, yticklabels=num_folds_range)
plt.xlabel('Número de Estimadores (n_estimators)')
plt.ylabel('Número de Folds (num_folds_range)')
plt.title('Mapa de Calor de MAE en función de Num Folds y Num Estimadores')
plt.show()
La razón por las que he parelelizado este algoritmo es simplemente porque tengo claro que es de una complejidad tan grande que soy consciente de que mi computador tardará bastante en evaluar algo así.
Estamos tomando 78 modelos distintos cuando cambiamos los ‘folds’ y 100 modelos extra por cada uno de estos donde probamos los distintos estimadores. Esto da un no menor total de 780 modelos de random forest utilizando validación cruzada y calculando el MAE en cada iteración … así que tengo por seguro que mi querido Charlie (el nombre de mi computador) tendrá una cuota de sufrimiento extra en nuestra aventura.
⏲️ 3 horas después …
Después de harto maquinar el cómo cumplir esta misión, el código finalmente entregó nuestro esperado resultado. Por supuesto, graficar 3 variables no es nada grato para nuestras mentes acostumbradas al 2D, así que hasta decidir cómo visualizar la información en este problema puede ser todo un desafío.
Pero somos aspirantes a aprendanzantes, así que ¡hay que avanzar … y no pierdas la disciplina que hemos tenido hasta ahora!
Después de mucho indagar al respecto, decidí que el mejor mecanismo de visualización para estos resultados era un mapa de calor (heatmap). Puedes visualizar en un plano bidimensional (folds y estimadores) distintos colores (MAE) que nos darán una idea de cómo tomar la decisión final para estos parámetros de nuestro modelo.
He puesto el heatmap en un formato html para que puedas interactuar con él y saques tus propias conclusiones hasta que llegue el siguiente capítulo. También lo dejé dispuesto un poco más abajo del post, pero creo que no se ve “bien” (sugiero mirar el enlace).
Supongo que ya ha sido suficiente por hoy y debemos descansar …
Hasta el próximo cronopunto del Principia 🥚.
DV

